今回はPart2です。よろしくお願いします。
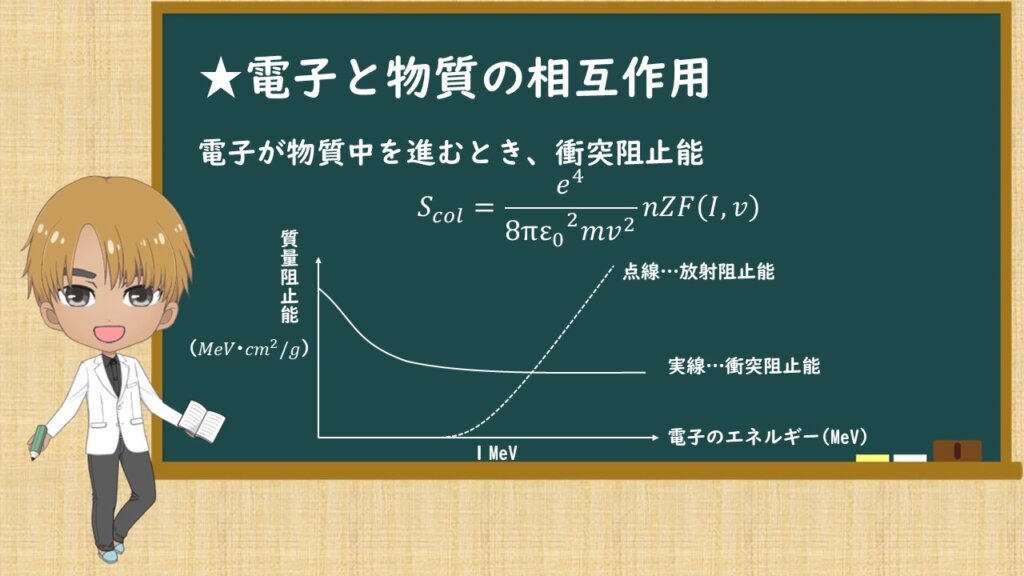
荷電粒子として、電子の場合についてです。荷電粒子の電子と物質の相互作用についてです。電子が物質中を進むときの衝突阻止能は黒板にある式になります。
F(I,v)は原子の平均励起エネルギー(I)と電子の速度(v)の関数です。
電子の質量阻止能を表したのが黒板にある図です。
前回の講義でも話したように、質量阻止能は、質量衝突阻止能と質量放射阻止能の和で表されるのと同じで、この図の放射阻止能と質量阻止能も同じです。
この図から覚えてほしいのは、電子の阻止能は放射阻止能と衝突阻止能の2つあるということ。電子のエネルギーが低いときは衝突阻止能の影響が大きく、エネルギーが大きくなると放射阻止能の影響も出てくるということです。
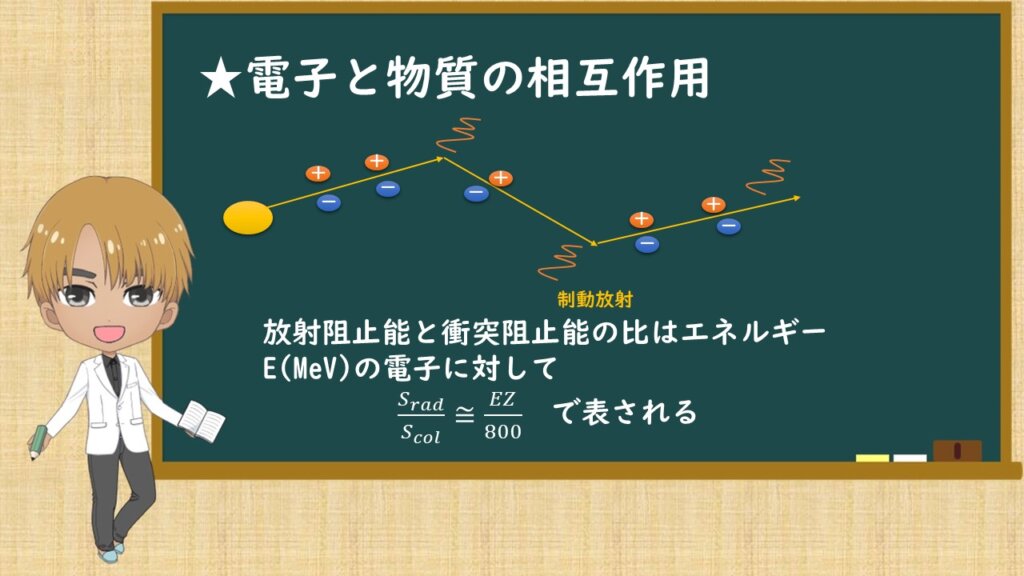
電子は、物質中を進んでいく中で物質の原子の電子もしくは、原子の原子核と相互作用します。原子核の電場により制動を受けると、制動放射によってエネルギーを失います。
エネルギーの高い電子ほど制動放射によるエネルギー損失の割合は大きくなります。そのため、1個前のスライドで前述したようになります。
放射阻止能と衝突阻止能の比はエネルギーEの電子に対して黒板にある式で表されます。Zは原子番号です。この式は覚えましょう。
さっきの図で衝突阻止能と放射阻止能の線が交わる点がありますね。その点は放射阻止能と衝突阻止能が等しくなる点であり、 Srad/Scol の値が1になり、1=EZ/800と書けます。
この関係はときどき計算で使います。

電子が物質中を進むとき、散乱によって方向を変えて進んでいきます。そのため、エネルギーが同じでも到達する深さは異なります。
(電子線では、方向を何度も変えて、入射してきた方向に戻っていく後方散乱があります。)
最も深く到達する距離を最大飛程といいます。

電子の飛程は到達する深さまでの距離なので単位は[cm]ですが、質量阻止能の時に阻止能を密度で割ったのを覚えていますか。
密度で割ると物質によらないって事は前回の講義でわかったと思います。
今回は、飛程は密度に反比例するので、飛程に密度をかけた g/cm2 単位で表すと、電子の最大飛程は物質にあまり依存しないことになります。
電子線の飛程ではこの単位[g/cm2]が用いられます。物質にあまり依存せず、エネルギーによって変わります。
入射エネルギーが0.8MeV以上の時、0.15~0.8MeVの時と変わってきます。
なぜ、エネルギーによって式が変わるかはなんとなく想像つくかもしれませんが、エネルギーによって相互作用のどの変化が起こりやすいか変わってきますね。エネルギーが高いほど制動放射によるエネルギー損失は大きかったですね。この式は覚えなくても大丈夫です。
そして、エネルギーによって飛程の式が変わりますが、遮蔽を求める場合などざっくりした計算でオレンジの式を使います。
この式は覚えておきましょう。電子の飛程聞かれたら、ざっくりこの式で計算すれば良いと思います。

電荷だけが違う陽電子についてです。陽電子については阻止能や飛程は電子の時と同じです。
しかし、陽電子は物質中でエネルギーを失い、止まるときに、物質中の電子と結合し、ポジトロニウムというものを形成します。
ポジトロニウムは短時間で消滅し、その消滅する際に、2本のエネルギー511keVの光子を反対方向に放出します。
これを電子対消滅といい、放出された光子のことを消滅放射線といいます。
陽電子の遮蔽を考えるときは、消滅放射線のことまで考えて遮蔽を考える必要があります。

次は、重荷電粒子と物質の相互作用です。これは、電子の場合と同様です。
しかし、重荷電粒子は質量が大きいので放射阻止能は通常無視できます。重荷電粒子では、放射阻止能は通常無視されるので、衝突阻止能のみになります。そのため、表記上、阻止能とだけしか書かれないです。
式としては黒板にあるようになります。この式は覚える必要はありません。

荷電粒子の質量をMとすると、衝突阻止能は黒板にある式のようになります。
重荷電粒子の阻止能を表した黒板の式は「ベーテの式」といわれ、荷電粒子の原子番号の2乗に比例し、速度の2乗に反比例します。
このオレンジの式は重要ですので覚えましょう。
荷電粒子は物質中では、エネルギーを失うまで方向をほとんど変えず、直進します。そしてエネルギーを失い、徐々に速度が小さくなります。

さっきのベーテの式より、阻止能が速度の2乗に反比例することから、止まりそうな時に、阻止能が非常に大きくなります。
ベーテの式でもわかるように、zは変化しないので定数で、vが徐々に0に近づくので、値が大きくなるのは式からもわかりますね。
グラフでもわかるように、その非常に大きくなった所をブラックピークといいます。止まる瞬間に起こるのがブラックピークになります。
グラフの縦軸の比電離は、飛跡にそって単位長さあたりの電離数を比電離といいます。

重荷電粒子の飛程は黒板にあるように与えられます。オレンジの式の部分は覚えましょう。
この式からもわかりますが、重荷電粒子はエネルギーを失うまでほぼ直進するので、同じ種類の重荷電粒子なら、同じエネルギーで物質中に入射させるとほぼ一定の距離で止まります。(電子の時は、ばらばらだったよね…)
この飛程も前に講義したのと同じです。エネルギー損失から求められます。
重荷電粒子の阻止能と飛程はよく試験に出ますし、式が似てるので混ざらないように気を付けてください。

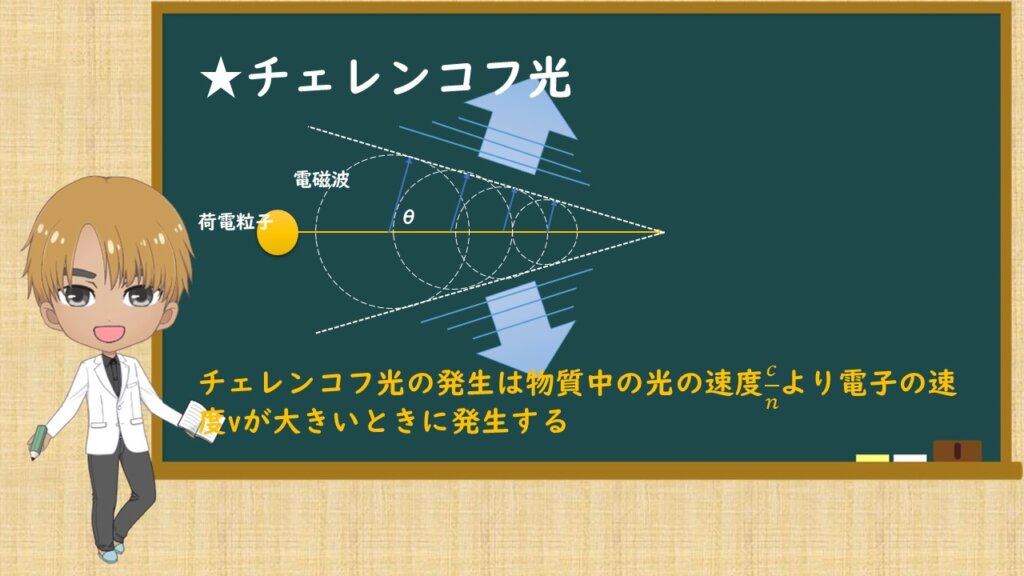
最後にチェレンコフ光についてです。
荷電粒子が物質中を通過すると、物質中の分子が荷電粒子の電場を感じて、その場で振動し、この振動により電磁波が発生します。
各点から発生した電磁波の波面がそろうことで、光として観測されます。これをチェレンコフ光といいます。
チェレンコフ光の発生は物質中の光の速度c/nより電子の速度vが大きいときに発生します。
これはですね、高校物理のレンズや光の屈折の範囲の話です。高校物理履修済みの方は忘れていたら振り返ってみて思い出してみてください。
習ってない方は、複雑なことは覚えず、黒板にある文言をまずは覚えておきましょう。
そのうち講義するかもしれません。(問題解説でもチェレンコフ光についてしっかりやります。)
以上で、荷電粒子と物質の相互作用を終わります。お疲れ様でした。




コメント