
こんにちは。今回は原子核の構造についてです。原子核の中の話になります。原子の構造でもお話しましたが、原子核は陽子と中性子で構成されています。
原子核についてより詳しくやって行きましょう。
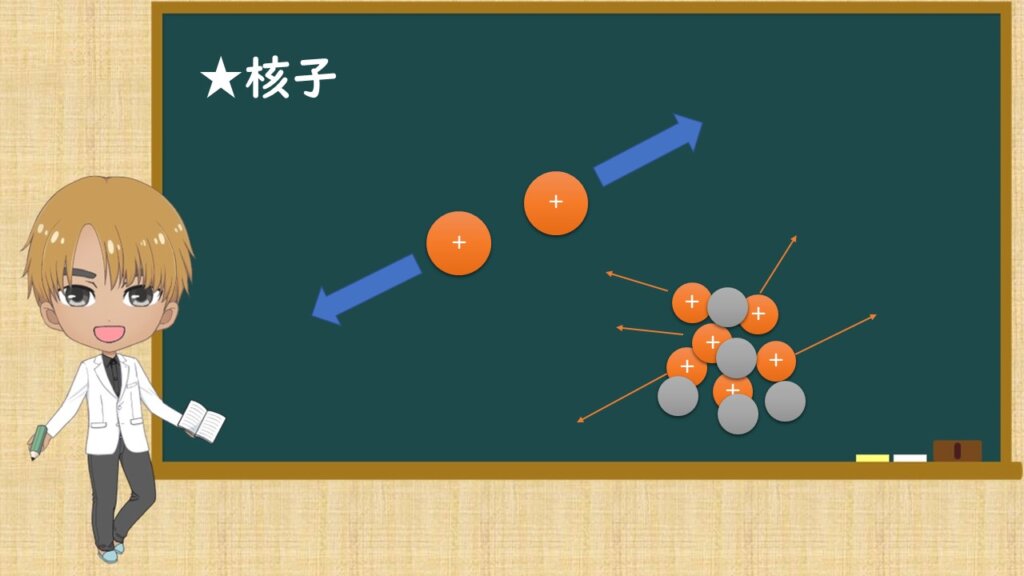
原子核内の陽子と中性子の事を核子といいます。
陽子は正電荷をもっており、普通に考えると、陽子と陽子があれば同じ電荷なので、電気的に反発すると思いませんか?
磁石を想像してもらうと、同じ極同士を近づければ近づけるほど、反発力は大きくなりますよね。
原子核なんてすごい小さく、陽子と陽子の距離なんてすごい小さいんですよ。反発力なんて大きいに決まってますよね。
そうすると原子核の中になんで陽子がたくさん存在できるんですかね??
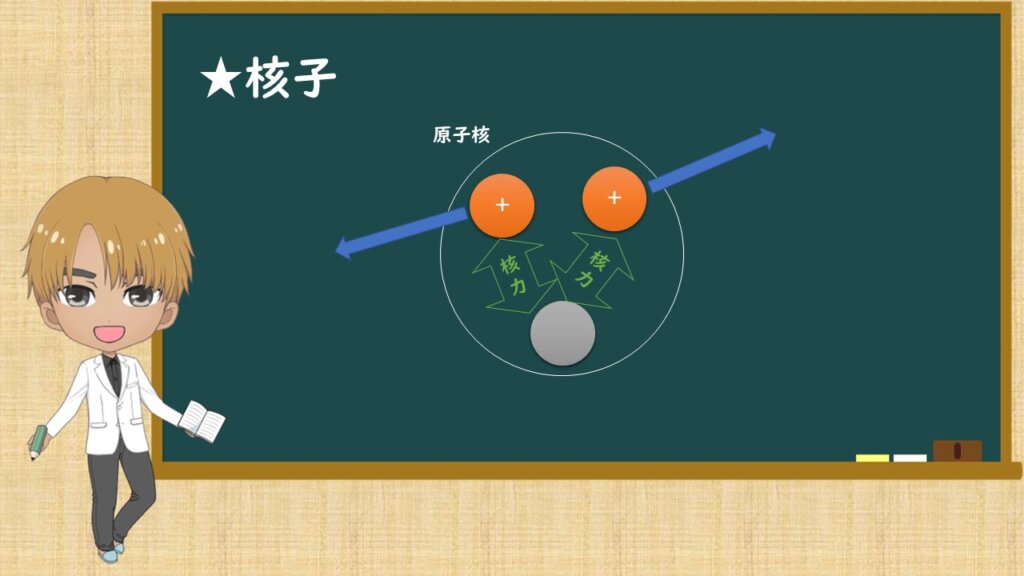
それはずばり、核力の影響です!!!
核子を原子核の中に閉じ込めている力を核力といいます。陽子と中性子の間で働いています。
電気的な反発力より、強い力で閉じ込めているのです。核力は強い力で、その力の及ぶ距離は短いです。

原子質量単位についてです。これは、質量数ではなく、実際の重さの話です。質量数は陽子と中性子の個数を足したもので、実際の重さではありません。
原子、原子核の質量を表すのに原子質量単位が用いられます。
これは、12Cの中性原子1個を12uと定めたものです。中性原子とは、陽子と軌道電子の数が等しい原子のことを言います。原子の電荷が±0なので中性ですね。
1uをエネルギー表記すると、黒板に示した通りになります。1uが931.5MeVであることは覚えておきましょう。実際になるか計算してみてください。

1uはほぼ核子の質量に等しいです。若干違うくらいですね。
それぞれエネルギーに換算すると、陽子は938.3MeV、中性子は939.6MeV、電子は0.511MeVとなります。この値は重要なので覚えておきましょう。

ここで、脱線します。さっきから、質量をエネルギーに変換せいていましたが、なんでそんなことできるの?質量とエネルギーいっぱい出てきて何を覚えたらいいの?
と思った方もいると思います。
実は、この式で質量からエネルギー、エネルギーから質量に換算しているのです。
この式は、1907年にアインシュタインの特殊相対性理論より発表された、質量とエネルギーの等価性の関係を表した式「E=mc2」があります。
これは、かっこよく言うと、「質量はエネルギーの形態の1つにすぎない」ということです。
要するに、エネルギーは質量を持つものに変わることがあるし、質量をもつものはエネルギーに変わることがあるということを示しています。
もっというと、質量には膨大なエネルギーをもっているということです。
面白い式、美しい式ですので、興味のある方は調べてみると良いと思います。実際に値を代入して計算してみても良いかもしれません。

原子質量単位をつかって、原子番号Z、中性子数Nの中性原子の質量Wを求めてみようっとなったとき、普通の感覚でいくと、
1.00726・Z+1.008665・N+0.000549・Zとなる
っと思うかもしれませんが、実は、その値にはならないず、小さい値になります。
それは、核子の核力が影響しています。核力による強い力によって束縛されているので、原子核内の位置エネルギーが低くなっているのです。
今の説明について詳しく話し始めると、時間がかなりかかってしまうのでここでは省きたいと思います。

実際の質量は、小さくなっていると言いました。
その質量の差は、上の式で表せます。
この式は、核力による束縛と電子のクーロン力による束縛の両方が影響していますが、クーロン力のよる質量差は、
核力による質量差に比べて無視できるため、原子核の質量差は
下の式になります。
この原子核の質量差を質量欠損といいます。

原子核の半径は黒板に示したようになります。この式は、重要ですので覚えましょう。言葉にすると、原子核の半径は、質量数の3分の1乗に比例すると言えます。
なぜ、3分の1乗なんでしょうか??これは難しくなく簡単です。
原子核の核子は核力で結びつけられていますが、力が及ぶ範囲は狭く、隣同士の核子までです。
核子がくっついている原子核の体積は核子の数に比例します。核子の数が多くなればなるほど、原子核の体積はその分大きくなります。
立方体で想像すると、体積がxの3乗なら、1辺の長さはxですよね。
体積がxなら、1辺の長さはxの3分の1乗になりますね。
これで3分の1乗の理由がわかったんじゃないですかね。

ここは、言葉の紹介です。
質量欠損をエネルギーに換算したものを結合エネルギーといいます。
そして、核子1個あたりの結合エネルギーを平均結合エネルギーといいます。
結合エネルギーはその名のとおり、核子が結合しているエネルギーです。たくさん言葉が出てきてややこしくなってる人もいったん落ち着いて言葉の意味をかみ砕いて理解できたら楽になると思います。
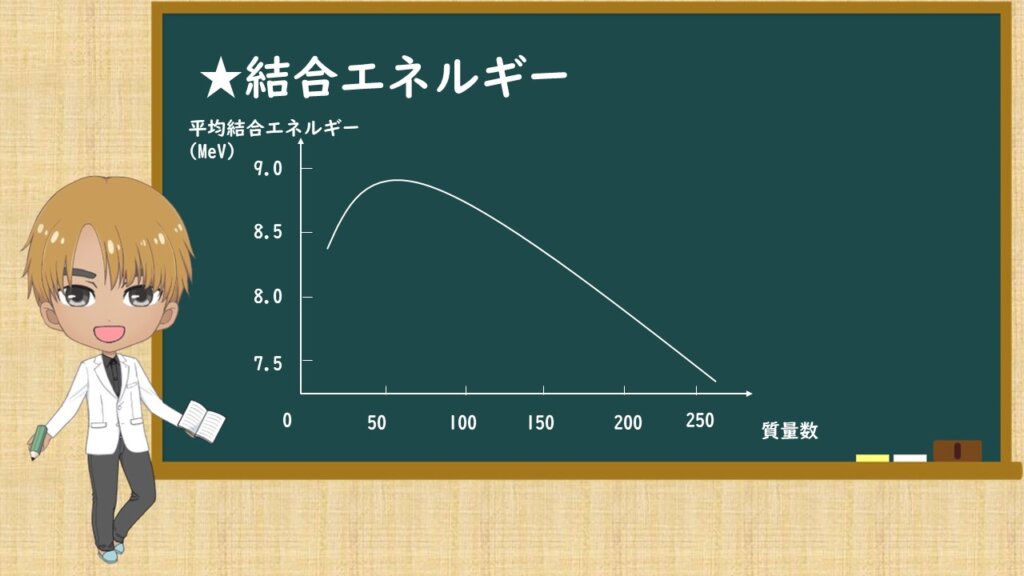
黒板にある図は、質量数に対する平均結合エネルギーです。
この図より、核子1個あたりの結合エネルギーはおよそ8MeVということです。重要です。
質量数の小さいところではどうなっているかというと、大きくなったり、小さくなったり、ジグザグしています。
4Heでおよそ7MeVをとります。
この図より次の特徴が言えます。

この3つの特徴は重要ですので覚えましょう。
他にも様々な特徴や、法則などがありますが(体積効果、表面効果、クーロン効果など)、ここでは試験でよく聞かれるところを覚えてきましょう。
平均結合エネルギーの性質って何に使われているのかというと、
核融合や核分裂の利用の元になっています。それについては後の講義で説明します。
以上で、原子核の構造についてはおしまいです。複雑なことは聞いたことあるなーぐらいで、覚えることをしっかり覚えましょう。お疲れ様でした。




コメント