
こんにちは。今回は光子と物質の相互作用Part2です。
Part2では光子の減衰と物質へのエネルギー伝達についてやっていこうと思います。
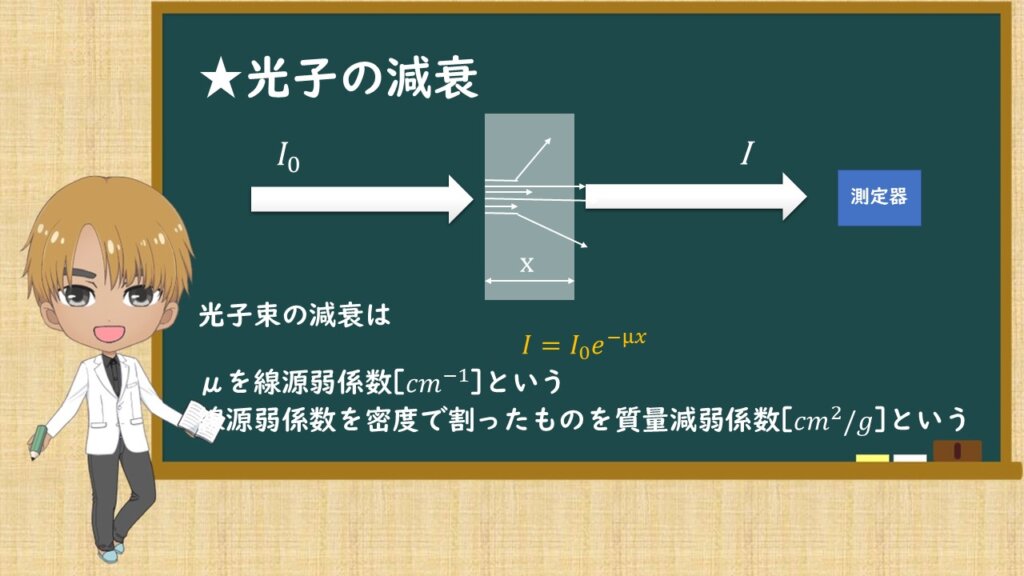
光子の減衰です。
光子が物質に照射されると、前回の講義でやった光電効果、コンプトン効果、電子対生成の3つの反応を起こします。
光子が物質にI0で入射させ、物質中で3つの反応を経て透過してきたIを測定器で測定してみると…
黒板にあるオレンジの式になります。これが光子の減弱です。
μを線源弱係数といい、線源弱係数を密度で割ったもの質量減弱係数といいます。密度で割る話はもう何回もやってきたので大丈夫ですね。
わからない方はこれまでの講義で何回か出てきてますので確認してください。

そして、I=I0/2となる物質の厚さを半価層といいます。さっきのオレンジの式に代入して計算すると、0.693/μになります。
これが半価層と線源弱係数の関係です。
半価層は、遮蔽能力の評価やX線、γ線の線質評価などに使用される指標になります。
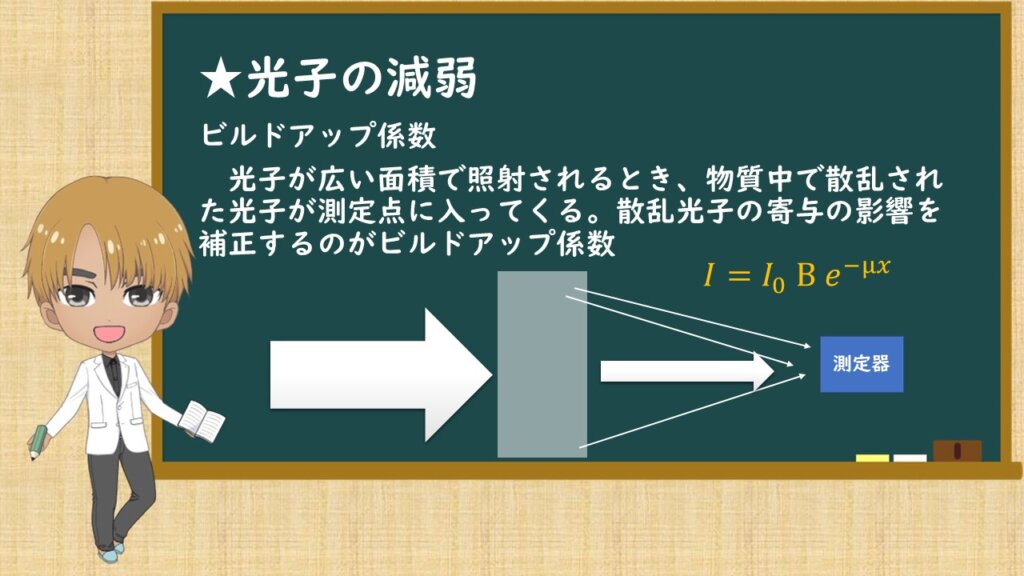
ビルドアップ係数についてです。
さっきまでは、ナロービーム(細いビーム)を物質に照射して、測定器で透過してきた光子を測定していました。
それが今回は、光子が広い面積で照射されるときです。物質中で散乱された光子が測定点に入ってくる。散乱光子の寄与の影響を補正するのがビルドアップ係数です。
オレンジの式では、Bがビルドアップ係数です。
基本的には、ビルドアップ係数を含んだ式が使われており、遮蔽が薄い場合や入射光子が細い場合、ビルドアップ係数は1とすることができ、
遮蔽の厚さや入射光子の太さが大きくなると、ビルドアップ係数は大きくなります。
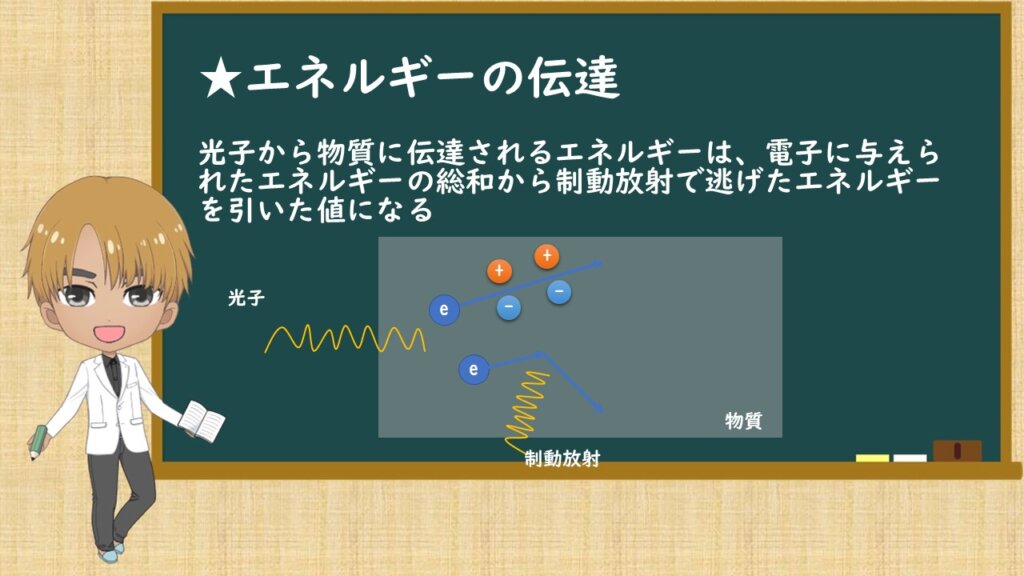
光子は、物質中で光電効果、コンプトン散乱、電子対生成などによって物質中の原子の軌道電子にエネルギーを与え、
そのエネルギーを得た軌道電子は物質中で電離や励起によって、物質にエネルギーを与えます。
この電子が物質中を進むときに、原子核の電場などで制動を受け制動放射を発生させます。制動放射は物質の外へ放射されます。
そのため、光子のエネルギー伝達は光子から物質に伝達されるエネルギーは、電子に与えられたエネルギーの総和から制動放射で逃げたエネルギーを引いた値になります。

光電効果、コンプトン効果、電子対生成それぞれでのエネルギー伝達による作用後の電子のエネルギーを考えてみます。
光電効果で発生する光電子のエネルギーは、入射光子のエネルギーから束縛エネルギーを引いた差になります。
コンプトン効果で発生する反跳電子のエネルギーは、散乱角度によって異なります。そのため平均エネルギーEとなります。
電子対生成では、電子と陽電子のエネルギーの和が光子エネルギーから電子の静止エネルギーの2倍を引いたものです。
それぞれの式をk0でくくって、式変形します。
それぞれの作用の断面積を用いると、エネルギー転移係数が求められ、黒板の式の様に書けます。もちろん、数字代入して計算とかわりません。
エネルギー転移係数は、係数とついていますが、文字通り、光子が物質にエネルギーをどれだけ転移(伝達)ができるかの係数です。
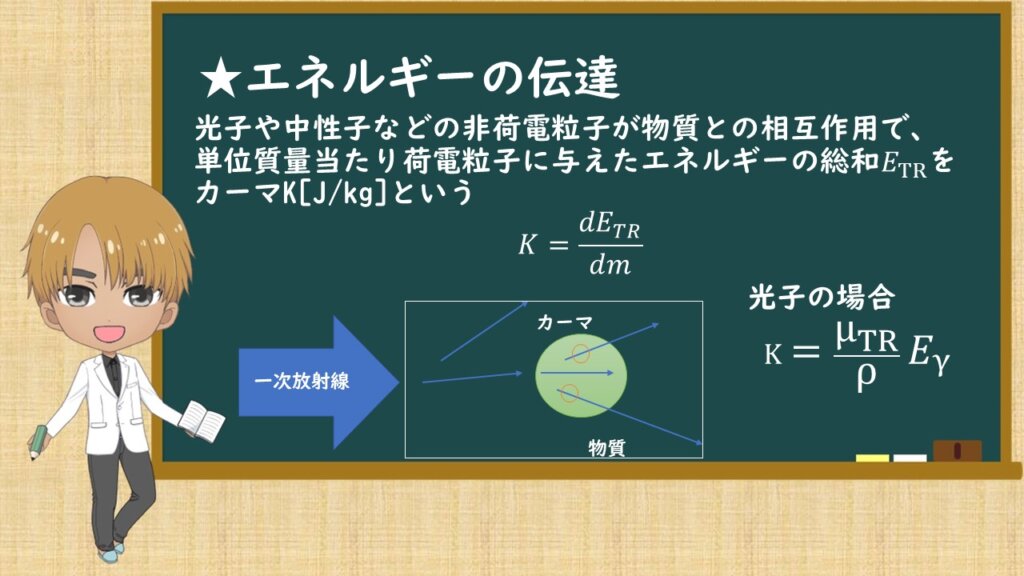
ここでは、「カーマ」についてです。かっこよく説明すると、光子や中性子などの非荷電粒子が物質との相互作用で、単位質量当たり荷電粒子に与えたエネルギーの総和ETRをカーマK[J/kg]といいます。
図で説明すると…
放射線(光子)が物質に照射されます。物質中で光子が相互作用によって散乱(いろんな方向に進んでいく)されます。相互作用する場所はばらばらです。入射してすぐ作用するのもあれば、入射してしばらく進んでから相互作用するのもあります。
(物質中の青い矢印は、相互作用によって発生した二次荷電粒子です。)
そこで、物質中全部を見てても、わかりにくいので、見る場所を決めます。
その物質の中で、ある範囲を決めます。(図でいう緑の円)
その円の中で相互作用し、光子が電子にエネルギーを伝達するのをカーマといいます。(オレンジの丸)
光子の場合、K=μTR/ρ ・Eγと書きます。エネルギー転移係数を密度で割り、光子のエネルギーをかけたのがカーマの計算式になります。
これは、先ほどのエネルギー転移係数の説明や、カーマの説明から、式を日本語で考えるとわかると思います。

物質中で、入射してきた光子が相互作用するのはもうわかりましたね。
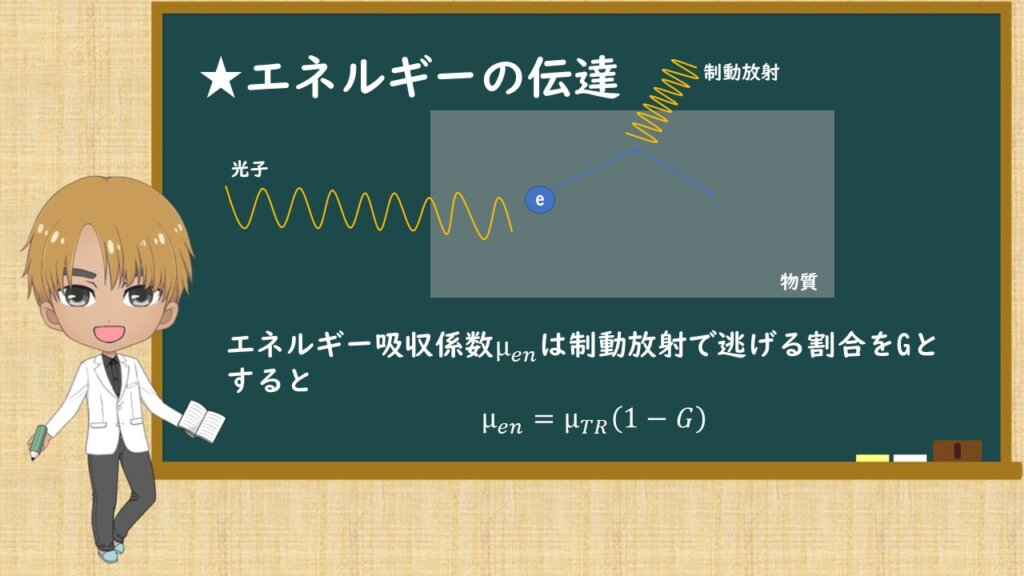
相互作用によって、エネルギーを得た電子が物質中を走り出します。そうすると、物質中の原子の原子核によって制動放射が起こります。
制動放射は、物質にとどまることはなく、物質の外へ放出されるので、物質のエネルギー吸収から引く必要があります。
エネルギー吸収係数μenは制動放射で逃げる割合をGとすると、黒板の式のように書けます。
この式だと、整理されててわかりにくいかもしれませんが、Gは制動放射の割合です。エネルギー転移係数にGをかけると制動放射のエネルギーになりますね。
すると、エネルギー吸収係数は、エネルギー転移係数から制動放射のエネルギーを引いたものになります。
光子のエネルギーが低い場合、制動放射で逃げていくエネルギーは小さくなります。そのため、エネルギー転移係数とエネルギー吸収係数はほぼ等しくなります。


さっきまではカーマの話をしていました。
今度は、「衝突カーマ」です。衝突っていう単語がつきました。
荷電粒子が物質中で制動放射を発生する割合をGとして、カーマから引いた値を衝突カーマKcといい、Kc=K(1-G)と書きます。
これは先ほどのエネルギー吸収係数のお話でやったのと同じですね。
そして、光子の場合、衝突カーマはエネルギー吸収係数を用いて、Kc=μen/ρ・Eγと書けます。この式も日本語でわかるようにしましょう。
これまでの説明を聞けばきっとできるはずです。
つぎは、放射線の量として用いられる、吸収線量と照射線量についてです。
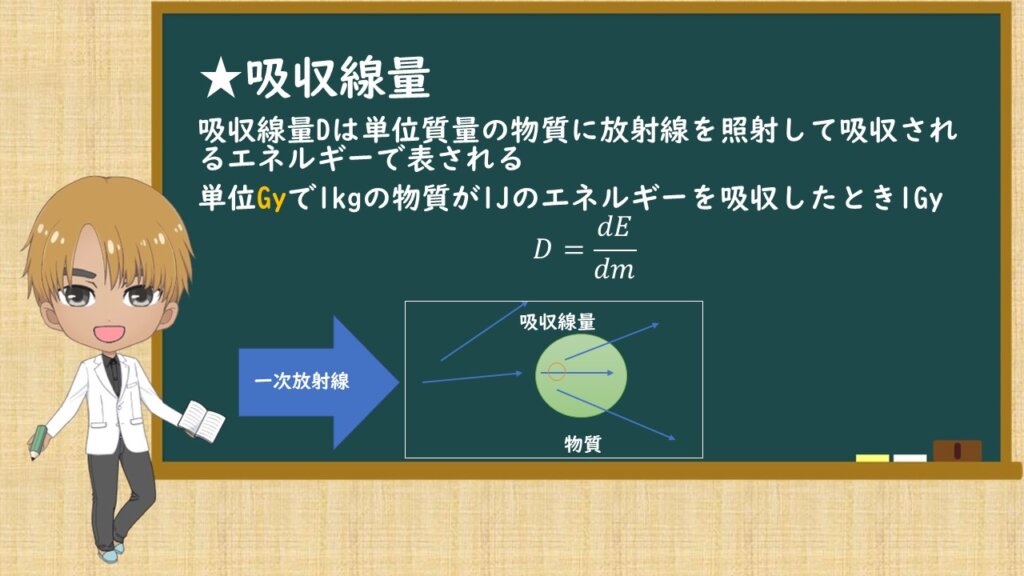
吸収線量は、放射線を物質に照射したときに、物質に吸収されるエネルギーのことです。
ここで、言葉の難しさに気を付けてください。放射線を照射した量ではないので気を付けてください。
図で説明します。この図はカーマの時の図と同じですが、着目している点が違います。(オレンジの丸)
吸収線量の着眼点は、領域内のエネルギー収支です。二次荷電粒子が発生し、それが領域内で吸収されたのを見ています。
単位はGy(グレイ)で、1kgの物質が1Jのエネルギーを吸収したとき1Gyといいます。

ここで、照射線量を説明する前に荷電粒子平衡について説明します。
さっきの図で、カーマと吸収線量で同じ図を用いましたが、
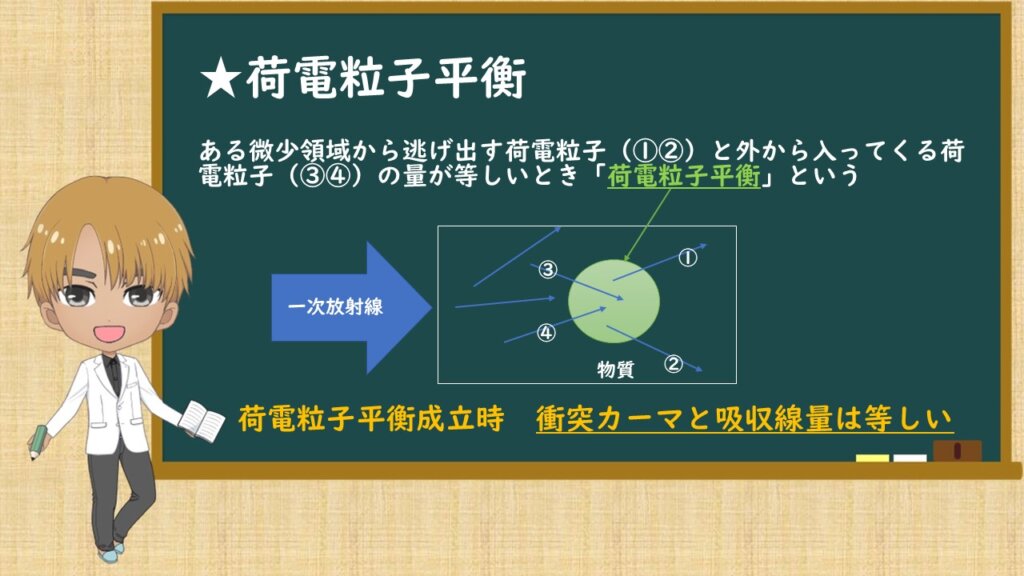
図と一緒に確認してみてください。ある微少領域から逃げ出す荷電粒子(①②)と外から入ってくる荷電粒子(③④)の量が等しいとき「荷電粒子平衡」といいます。
荷電粒子平衡が成立しているとき、衝突カーマと吸収線量は等しくなります。あまり、わかって無くても、荷電粒子平衡がどういう状態なのかということと、この文言で覚えておくといいかもしれません。
荷電粒子平衡は放射線の測定などで使われますので、その時にまた講義します。


照射線量です。
光子で物質を照射したときに空気中に生じた電荷の量を照射線量といいます。
単位はC(クーロン)/kgです。
空気1kgを照射して1C(クーロン)の電荷を生じたとき照射線量は1C/kgで表されます。
照射線量をW値を用いて吸収線量に変換することができます。そのような問題も出題されてますので、問題解説の時に見ていきましょう。
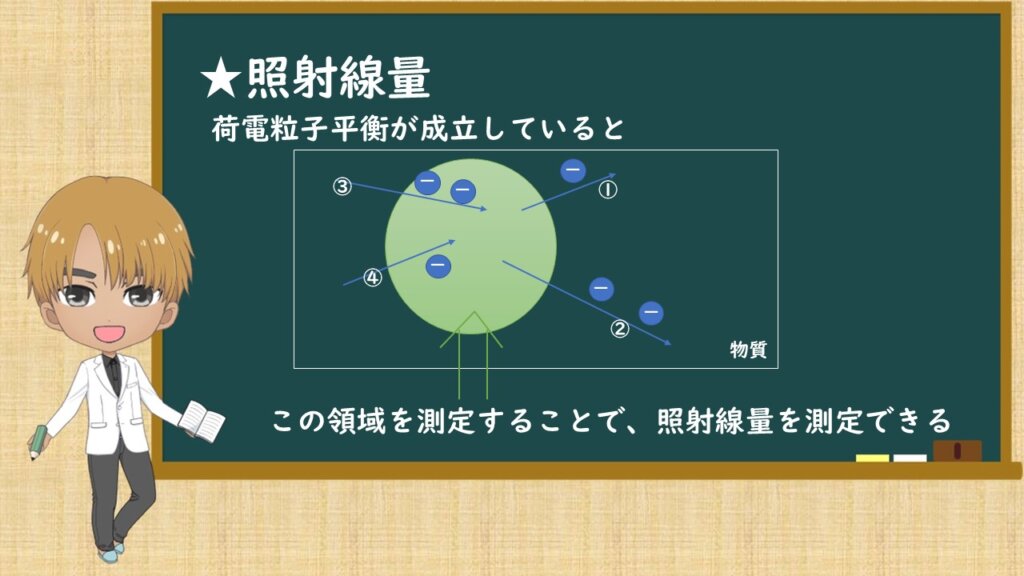
そして、荷電粒子平衡が成立しているとき、
領域外で発生した電子により領域内で発生する電荷量(③④)と、領域内で発生した電子により領域外で発生する電荷量が等しいので、領域を測定すると、照射線量を測定することができます。
以上で、光子と物質の相互作用Part2は終わりです。荷電粒子と物質の相互作用としっかり区別して覚えましょう。お疲れ様でした。





コメント